|
Спектр
генерации лазера
Автор:
С.П.
Воробьев
Часть I. Формирование спектра генерации
лазера.
 1.1.
Виды спектров. 1.1.
Виды спектров.
На первый взгляд лазерный пучок кажется
очень простым по своей структуре. Это
практически одночастотное излучение, имеющее
спектрально чистый цвет: He-Ne лазер имеет
излучение красного цвета (633 нм), кадмиевый
лазер излучает синий цвет (440 нм, аргоновый
лазер излучает несколько линий в
сине-зеленой области спектра (488 нм, 514 нм
и др.), полупроводниковый лазер – красное
излучение (650 нм) и т.д.
 На
самом деле спектр излучения лазера имеет
довольно сложную структуру и определяется
двумя параметрами – спектром излучения
рабочего вещества (для He-Ne лазера,
например, это красная спектральная линия
излучения неона, возбужденного электрическим
разрядом) и резонансными явлениями в
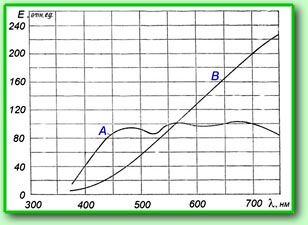
оптическом резонаторе лазера. Для сравнения,
на рисунках справа приведены спектры
излучения солнца (A) и обычной лампочки
накаливания (B) (верхний рис.), спектр
ртутной лампы (рис. справа) и сильно
увеличенный спектр генерации He-Ne лазера
(рис. внизу). На
самом деле спектр излучения лазера имеет
довольно сложную структуру и определяется
двумя параметрами – спектром излучения
рабочего вещества (для He-Ne лазера,
например, это красная спектральная линия
излучения неона, возбужденного электрическим
разрядом) и резонансными явлениями в
оптическом резонаторе лазера. Для сравнения,
на рисунках справа приведены спектры
излучения солнца (A) и обычной лампочки
накаливания (B) (верхний рис.), спектр
ртутной лампы (рис. справа) и сильно
увеличенный спектр генерации He-Ne лазера
(рис. внизу).
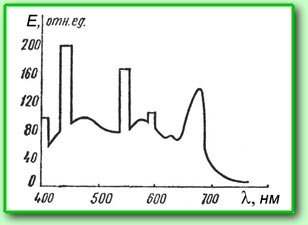
 Спектр
лампы накаливания, как и солнечный спектр,
относится к непрерывным спектрам, которые
полностью заполняет видимый спектральный
диапазон электромагнитного излучения
(400-700 нм). Спектр ртутной лампы относится
к линейчатым спектрам, который так же
заполняет весь видимый диапазон, но состоит
из отдельных спектральных компонент
различной интенсивности. Кстати, до
появления лазеров монохроматическое
излучение получали, выделяя отдельные
спектральные компоненты излучения ртутной
лампы. Спектр
лампы накаливания, как и солнечный спектр,
относится к непрерывным спектрам, которые
полностью заполняет видимый спектральный
диапазон электромагнитного излучения
(400-700 нм). Спектр ртутной лампы относится
к линейчатым спектрам, который так же
заполняет весь видимый диапазон, но состоит
из отдельных спектральных компонент
различной интенсивности. Кстати, до
появления лазеров монохроматическое
излучение получали, выделяя отдельные
спектральные компоненты излучения ртутной
лампы.
1.2.
Спектр
излучения
в He-Ne
лазере.
 Спектр
излучения лазера является монохроматическим,
т. е. имеет очень узкую спектральную ширину,
но, как видно из рисунка, он так же имеет
сложную структуру [9].
Процесс формирования лазерного спектра
рассмотрим на основе хорошо изученного He-Ne
лазера. Исторически это был первый лазер
непрерывного действия, работающий в видимом
диапазоне спектра. Он был создан А. Джаваном
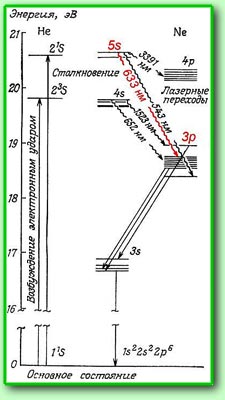
в 1960 г. На рис. справа показаны
энергетические уровни возбужденной смеси
гелия и неона [10]. Возбужденный атом гелия
или неона – это атом, у которого один или
несколько электронов внешней оболочки при
столкновениях с электронами и ионами
газового разряда переходят на более высокие
энергетические уровни и в дальнейшем могут
перейти на более низкий энергетический
уровень или вернуться обратно, на
нейтральный уровень, с испусканием светового
кванта – фотона. Спектр
излучения лазера является монохроматическим,
т. е. имеет очень узкую спектральную ширину,
но, как видно из рисунка, он так же имеет
сложную структуру [9].
Процесс формирования лазерного спектра
рассмотрим на основе хорошо изученного He-Ne
лазера. Исторически это был первый лазер
непрерывного действия, работающий в видимом
диапазоне спектра. Он был создан А. Джаваном
в 1960 г. На рис. справа показаны
энергетические уровни возбужденной смеси
гелия и неона [10]. Возбужденный атом гелия
или неона – это атом, у которого один или
несколько электронов внешней оболочки при
столкновениях с электронами и ионами
газового разряда переходят на более высокие
энергетические уровни и в дальнейшем могут
перейти на более низкий энергетический
уровень или вернуться обратно, на
нейтральный уровень, с испусканием светового
кванта – фотона.
Возбуждение атомов производится
электрическим током, проходящим через
газовую смесь. Для He-Ne лазера это
слаботоковый, тлеющий разряд (типичные токи
разряда – 20-50 мА). Картина энергетических
уровней и механизм излучения достаточно
сложны даже для такого "классического"
лазера, которым является He-Ne лазер,
поэтому мы ограничимся рассмотрением только
основных деталей этого процесса. Атомы
гелия, возбужденные до уровня 2S при
столкновениях с атомами неона передают им
накопленную энергию, возбуждая их до уровня
5S (поэтому гелия в газовой смеси больше,
чем неона). С уровня 5S электроны могут
перейти на ряд более низких энергетических
уровней. Нас интересует только переход 5S –
3P (оба уровня в действительности расщеплены
на ряд подуровней из-за квантовой природы
механизмов возбуждения и излучения). Длина
волны излучения фотонов при этом переходе –
633 нм. Отметим еще один важный факт,
принципиально важный для получения
когерентного излучения. При правильно
подобранных пропорции гелия и неона,
давлении смеси газов в трубке и величине
разрядного тока электроны накапливаются на
уровне 5S и их количество превышает
количество электронов, находящихся на нижнем
уровне 3P. Это явление называется инверсной
заселенностью уровня. Однако, это пока еще
не лазерное излучение. Это одна из
спектральных линий в спектре излучения
неона. Ширина спектральной линии зависит от
нескольких причин, главные из которых: -
конечная ширина энергетических уровней (5S и
3P), участвующих в излучении и определяемая
квантовым принципом неопределенности,
связанным со временем пребывания атомов
неона в возбужденном состоянии, - уширение
линии связанное с постоянным движением
возбужденных частиц в разряде под
воздействием электрического поля (так
называемый эффект Доплера). С учетом этих
факторов ширина линии (специалисты называют
ее контуром рабочего перехода) равна
примерно двум десятитысячным ангстрема. Для
таких узких линий в расчетах удобнее
использовать ее ширину в частотной области.
Воспользуемся формулой перехода:
dn1=dlc/l2
(1)
где dn1
- ширина спектральной линии в частотной
области, Гц, dl -
ширина спектральной линии (0,000002 нм),
l
- длина волны спектральной линии (633нм), c
– скорость света. Подставив все значения (в
одной системе измерения), получим ширину
линии 1,5 ГГц. Конечно, такую узкую линию
можно считать вполне монохроматической по
сравнению со всем спектром излучения неона,
но назвать это когерентным излучением еще
нельзя. Для получения когерентного излучения
в лазере используется оптический резонатор
(интерферометр).
1.3. Оптический резонатор лазера.
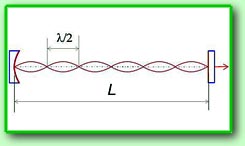 Оптический
резонатор представляет собой два зеркала,
находящихся на оптической оси и обращенных
отражающими поверхностями друг к другу, рис.
справа. Зеркала могут быть плоскими или
сферическими. Плоские зеркала очень трудно
юстировать и генерация лазерного излучения
может быть нестабильной. Резонатор со
сферическими зеркалами (конфокальный
резонатор) гораздо стабильнее, но пучок
лазера может быть неоднородным по сечению
из-за сложного, многомодового состава
излучения. На практике чаще всего используют
полуконфокальный резонатор с задним
сферическим и передним плоским зеркалом.
Такой резонатор относительно стабилен и дает
однородный (одномодовый) пучок. Оптический
резонатор представляет собой два зеркала,
находящихся на оптической оси и обращенных
отражающими поверхностями друг к другу, рис.
справа. Зеркала могут быть плоскими или
сферическими. Плоские зеркала очень трудно
юстировать и генерация лазерного излучения
может быть нестабильной. Резонатор со
сферическими зеркалами (конфокальный
резонатор) гораздо стабильнее, но пучок
лазера может быть неоднородным по сечению
из-за сложного, многомодового состава
излучения. На практике чаще всего используют
полуконфокальный резонатор с задним
сферическим и передним плоским зеркалом.
Такой резонатор относительно стабилен и дает
однородный (одномодовый) пучок.
Главным свойством любого резонатора является
образование в нем стоячих электромагнитных
волн. В случае He-Ne лазера стоячие волны
образуются для излучения спектральной линии
неона с длиной волны 633 нм. Этому
способствует максимальный коэффициент
отражения зеркал, подобранный как раз для
этой длины волны. В лазерных резонаторах
используются диэлектрические зеркала с
многослойным напылением, позволяющим
получить коэффициент отражения 99% и выше.
Как известно, условие образования стоячих
волн заключается в том, что расстояние между
зеркалами должно быть равно целому числу
полуволн:
nl=2L
(2)
где n – целое число или порядок
интерференции,
l – длина волны
излучения внутри интерферометра, L –
расстояние между зеркалами.
Из условия резонанса (2) можно получить
расстояние между резонансными частотами dn2:
dn2=c/2L
(3)
Для полутораметрового резонатора газового
лазера (He-Ne лазер ЛГН-220) эта величина
составляет примерно 100 МГц. Только
излучение с таким частотным периодом может
многократно отражаться от зеркал резонатора
и усиливаться по мере прохождения через
инверсную среду - возбужденную электрическим
разрядом смесь гелия и неона. Причем, что
чрезвычайно важно, при прохождении этого
излучения вдоль резонатора, его фазовая
структура не изменяется, что приводит к
когерентным свойствам усиленного излучения.
Этому способствует инверсная заселенность
уровня 5S, о которой говорилось выше.
Электрон с верхнего уровня переходит на
нижний синхронно с фотоном, инициирующим
этот переход, поэтому фазовые параметры
волн, соответствующих обоим фотонам
одинаковы. Такая генерация когерентного
излучения происходит по всему пути излучения
внутри резонатора. Кроме того, резонансные
явления приводят к гораздо большему сужению
линии излучения, в результате чего
наибольшее усиление получается в центре
резонансного пика.
Через определенное число проходов
интенсивность когерентного излучения
становится настолько высокой, что превышает
естественные потери в резонаторе (рассеяние
в активной среде, потери на зеркалах,
дифракционный потери и т.д.) и часть его
выходит за пределы резонатора. Для этого
выходное, плоское зеркало сделано с немного
меньшим коэффициентом отражения
(99,6-99,7%). В результате спектр генерации
лазера имеет вид, показанный на третьем рис.
сверху. Число спектральных компонент обычно
не превышает десяти.
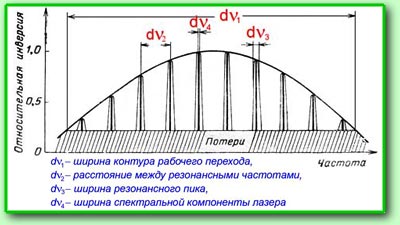
Просуммируем еще раз все факторы,
определяющие частотные характеристики
излучения лазера. Прежде всего, рабочий
переход характеризуется естественной шириной
контура. В реальных условиях за счет
различных факторов контур уширяется. В
пределах уширенной линии размещаются
резонансные линии интерферометра, число
которых определяется шириной контура
перехода и расстоянием между соседними
пиками. Наконец, в центре пиков
располагаются чрезвычайно узкие спектральные
линии излучения лазера, которые и определяют
спектр выходного излучения лазера.
1.4. Когерентность лазерного излучения.
Уточним, какую длину когерентности
обеспечивает излучение He-Ne лазера.
Воспользуемся формулой, предложенной в
работе [11]:
по мере прохождения через инверсную среду -
возбужденную электрическим разрядом смесь
гелия и неона. Причем, что чрезвычайно
важно, при прохождении этого излучения вдоль
резонатора, его фазовая структура не
изменяется, что приводит к когерентным
свойствам усиленного излучения. Этому
способствует инверсная заселенность уровня
5S, о которой говорилось выше. Электрон с
верхнего уровня переходит на нижний
синхронно с фотоном, инициирующим этот
переход, поэтому фазовые параметры волн,
соответствующих обоим фотонам одинаковы.
Такая генерация когерентного излучения
происходит по всему пути излучения внутри
резонатора. Кроме того, резонансные явления
приводят к гораздо большему сужению линии
излучения, в результате чего наибольшее
усиление получается в центре резонансного
пика.
dt=dn-1
(4)
где dt - время
когерентности, представляющее собой верхний
предел временного интервала, на котором
амплитуда и фаза монохроматической волны
являются постоянными. Перейдем к привычной
для нас длине когерентности l, с помощью
которой легко оценивать глубину записываемой
на голограмме сцены:
l=c/dn
(5)
Подставляя данные в формулу (5), в т.ч.,
полную ширину спектра dn1
= 1,5 ГГц, получим длину когерентности 20
см. Это довольно близко к реальной длине
когерентности He-Ne лазера, имеющего
неизбежных потери излучения в резонаторе.
Измерения длины когерентности с помощью
интерферометра Майкельсона дают величину
15-17 см (на уровне 50%-го уменьшения
амплитуды интерференционной картины).
Интересно оценить длину когерентности
отдельной спектральной компоненты,
выделенной резонатором лазера. Ширина
резонансного пика интерферометра dn3
(см. третий сверху рис.) определяется его
добротностью и равна примерно 0,5 МГц. Но,
как говорилось выше, резонансные явления
приводят к еще большему сужению лазерной
спектральной линии dn4,
формирующейся вблизи центра резонансного
пика интерферометра (третий сверху рис.).
Теоретический расчет дает ширину линии
восемь тысячных герца! Однако эта величина
не имеет большого практического смысла, так
как для длительного существования такой
узкой спектральной компоненты необходимы
значения механической стабильности
резонатора, теплового дрейфа и других
параметров, которые абсолютно невозможны в
реальных условиях эксплуатации лазера.
Поэтому мы ограничимся шириной резонансного
пика интерферометра. Для ширины спектра 0,5
МГц длина когерентности, рассчитанная по
формуле (5) равна 600 м. Это тоже очень
неплохо. Остается только выделить одну
спектральную компоненту, оценить ее мощность
и удержать ее на одном месте. Если же она за
время экспонирования голограммы "пройдется"
по всему рабочему контуру (по причине,
например, температурной нестабильности
резонатора), мы опять получим те же 20 см
когерентности.
1.5. Спектр генерации ионного лазера.
Расскажем коротко о спектре генерации
другого газового лазера – аргонового. Этот
лазер, как и криптоновый, относится к ионным
лазерам, т.е. в процессе генерации
когерентного излучения участвуют уже не
атомы аргона, а их ионы, т. е. атомы, один
или несколько электронов внешней оболочки
которого оторваны под воздействием мощного
дугового разряда, который проходит через
активное вещество. Ток разряда достигает
нескольких десятков ампер, электрическая
мощность блока питания – несколько десятков
киловатт. Необходимо обязательное
интенсивное водяное охлаждение активного
элемента, иначе произойдет его тепловое
разрушение. Естественно, в таких жестких
условиях картина возбуждения атомов аргона
еще более сложная. Возникает генерация сразу
нескольких лазерных спектральных линиях,
ширина рабочего контура каждой из них
существенно больше ширины контура линии
He-Ne лазера и составляет несколько
гигагерц. Соответственно, длина
когерентности лазера уменьшается до
нескольких сантиметров. Для записи голограмм
большого формата необходима частотная
селекция спектра генерации, о чем пойдет
речь во второй части этой статьи.
1.6. Спектр генерации полупроводникового
лазера.
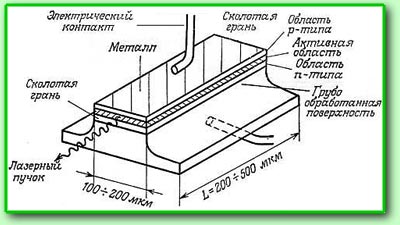 Перейдем
к рассмотрению спектра генерации
полупроводникового лазера, представляющего
большой интерес для процесса обучения
голографии и для начинающих голографистов.
Исторически первыми были разработаны
инжекционные полупроводниковые лазеры на
основе арсенида галия, рис. справа. Перейдем
к рассмотрению спектра генерации
полупроводникового лазера, представляющего
большой интерес для процесса обучения
голографии и для начинающих голографистов.
Исторически первыми были разработаны
инжекционные полупроводниковые лазеры на
основе арсенида галия, рис. справа.
Так как его конструкция достаточно проста,
рассмотрим принцип работы полупроводникового
лазера на его примере. Активным веществом, в
котором происходит генерация излучения,
является монокристалл арсенида галия,
имеющий форму параллепипеда со сторонами
длиной несколько сотен микрон. Две боковые
грани делаются параллельными и полируются с
высокой степенью точности. За счет большого
показателя преломления (n = 3,6), на границе
кристалл-воздух получается достаточно
большой коэффициент отражения (около 35%),
что достаточно для получения генерации
когерентного излучения без дополнительного
напыления отражающих зеркал. Две другие
грани кристалла скошены под некоторым углом;
через них индуцированное излучение не
выходит. Генерация когерентного излучения
происходит в p-n переходе, который создается
путем диффузии акцепторных примесей (Zn, Cd
и др.) в область кристалла, легированную
донорными примесями (Te, Se и др.). Толщина
активной области в перпендикулярном к p-n
переходу направлении составляет около 1 мкм.
К сожалению, в такой конструкции
полупроводникового лазера пороговая
плотность тока накачки оказывается
достаточно большой (около 100 тыс. ампер на
1 кв.см.). Поэтому этот лазер мгновенно
разрушается при работе в непрерывном режиме
при комнатной температуре и требует сильного
охлаждения. Лазер стабильно работает при
температуре жидкого азота (77 K) или гелия
(4,2K).
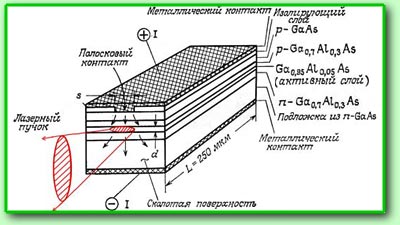 Современные
полупроводниковые лазеры делают на базе
двойных гетеропереходов, рис. справа. В
такой структуре пороговую плотность тока
удалось уменьшить на два порядка, до 1000
А/см. кв. При такой плотности тока возможна
стабильная работа полупроводникового лазера
и при комнатной температуре. Первые образцы
лазеров работали в инфракрасном диапазоне
(850 нм). При дальнейшем совершенствовании
технологии формирования полупроводниковых
слоев, появились лазеры как с увеличенной
длиной волны (1.3 – 1,6 мкм) для
оптоволоконных линий связи, так и с
генерацией излучения в видимой области (650
нм). Уже существуют лазеры, излучающие в
синей области спектра. Большим преимуществом
полупроводниковых лазеров является их
высокий КПД (соотношение энергии излучения к
электрической энергии накачки), которое
доходит до 70%. Для газовых лазеров, как для
атомарных, так и ионных, КПД не превышает
0,1%. Современные
полупроводниковые лазеры делают на базе
двойных гетеропереходов, рис. справа. В
такой структуре пороговую плотность тока
удалось уменьшить на два порядка, до 1000
А/см. кв. При такой плотности тока возможна
стабильная работа полупроводникового лазера
и при комнатной температуре. Первые образцы
лазеров работали в инфракрасном диапазоне
(850 нм). При дальнейшем совершенствовании
технологии формирования полупроводниковых
слоев, появились лазеры как с увеличенной
длиной волны (1.3 – 1,6 мкм) для
оптоволоконных линий связи, так и с
генерацией излучения в видимой области (650
нм). Уже существуют лазеры, излучающие в
синей области спектра. Большим преимуществом
полупроводниковых лазеров является их
высокий КПД (соотношение энергии излучения к
электрической энергии накачки), которое
доходит до 70%. Для газовых лазеров, как для
атомарных, так и ионных, КПД не превышает
0,1%.
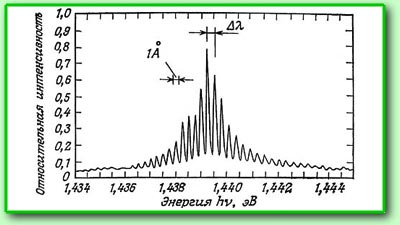 В
связи со спецификой процесса генерации
излучения в полупроводниковом лазере, ширина
спектра излучения гораздо больше ширины
спектра He-Ne лазера, рис. справа. В
связи со спецификой процесса генерации
излучения в полупроводниковом лазере, ширина
спектра излучения гораздо больше ширины
спектра He-Ne лазера, рис. справа.
Ширина рабочего контура составляет около 4
нм. Число спектральных гармоник может
достигать нескольких десятков. Это
накладывает серьезное ограничение на длину
когерентности лазера. Если воспользоваться
формулами (1), (5), теоретическая длина
когерентности составит всего 0,1 мм. Однако,
как показали прямые измерения длины
когерентности на интерферометре Майкельсона
и запись отражающих голограмм, реальная
длина когерентности полупроводниковых
лазеров доходит до 4-5 см. Это говорит о
том, что реальный спектр генерации
полупроводникового лазера не так богат
гармониками и имеет не такую большую ширину
контура рабочего перехода, как предсказывает
теория. Однако, справедливости ради, стоит
заметить, что степень когерентности
излучения полупроводниковых лазеров сильно
меняется как от образца к образцу, так и от
режима его работы (величина тока накачки,
условия охлаждения и т.д. Поэтому необходим
обязательный контроль параметров спектра
излучения в процессе подготовки
полупроводникового лазера к записи
голограммы.
-->
|



