|
5. Beam polarization
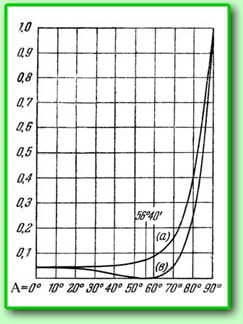 It is well known that light
which is reflected from the glass plate depends
on the angle of incidence: the larger angle, the
larger degree of reflection: from 4% at a normal
incidence up to 100% at sliding incidence, when
the beam is practically parallel with the plate,
see the graphical chart, upper curve.
Laser radiation is coherent and polarized. Light
reflection in the photoplate for coherent light
has very complicated nature because of multiple
inner reflections, see fig. below. The beams which
are reflected from the lower and upper planes of
the photoplate interfere and this causes parasite
interference pattern that makes worse the picture.
Since there are some small variations of photoplate's
width, this pattern looks like strips on the tree
cut and this picture is called "dendriform",
see the photo below.
Vector of the laser beam polarization is located
in the plane which is perpendicular to the direction
of beam spreading. If this vector of polarization
is located in the incidence plane (the incidence
plane is the plane formed by normal to the photoplate
and the beam axis), there is a special angle - Brewster
angle. The 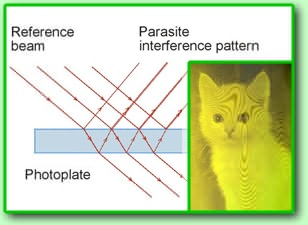 beam reflections from the
photoplate disappear for Brewster angle, see the
graphical chart, lower curve. The beam passes through
the photoplate without reflection! Brewster angle
depends on refraction index of the photoplate's
glass substrate and it is calculated according to
the following formula:
tg(A)
= n,
where
n is refraction index of the photoplate, A - angle
of the beam incidence in air.
Refraction index of the glass, which is used for
the photoplate substrate, is equal to 1.52. Gelatine
layer has approximately the same refraction index.
The equation gives the result:
A =
56.60
 Reference beam should fall
on the photoplate exactly under this angle, in order
to obtain pure holographic image, see figure.
It's not difficult to adjust Brewster angle. You
may use polarizer and determine the plane where
is located the vector of laser polarization. If
you need, it is possible to turn the plane by rotating
the laser itself (if its design allows this) or
turn the plate of polarization using a semi-wave
plate. In our case, polarization vector of He-Ne
laser radiation is located in the vertical plane
therefore the recording beam is formed in the vertical
plane too (see Lesson 1).
Then put an ordinary glass plate under the laser
beam and observe reflected light on a sheet of white
paper. Black paper should be placed under the plate,
and the light in a room should be switched off,
because reflected light is not intensive. If you
change the angle of photoplate illumination, you'll
see that intensity of reflected light varies also.
Brewster angle is the angle under which intensity
of reflected light will be minimal or disappear
completely.
References
M. Born, E. Wolf, " Principles of Optics",
New York.
-->
|
