|
Пространственная
Фурье-спектроскопия
Автор:
Н.Г.
Власов, А.Е. Штанько
Дается краткий обзор нового направления в спектральных
измерениях – пространственной Фурье-спектроскопии,
приводится принципиальная оптическая схема соответствующего
прибора и результаты экспериментов, подтверждающих
его работоспособность.
Фурье-спектроскопия широко применяется для решения
различных научно-технических задач
[1-3]. Ее преимуществом,
по сравнению с конкурирующими спектральными
методами, является регистрация светового потока
как единого целого, не разложенного предварительно
в спектр. Напомним, что в Фурье-спектроскопии
точечным приемником регистрируется и затем обрабатывается
интерферограмма – взаимная интенсивность объектного
и опорного волновых полей. Временная задержка
(разность оптических путей) между этими полями
непрерывно изменяется в соответствии с движением
зеркала в интерферометре Майкельсона. Таким
образом, несмотря на достоинства и широкое применение,
к очевидным недостаткам Фурье-спектроскопии
относится невозможность исследования быстропротекающих
процессов и необходимость использования высокоточной
механики, обеспечивающей равномерное прямолинейное
движение одного из зеркал интерферометра.
В связи с этим представляется несомненно актуальным
разработка пространственного аналога Фурье-спектроскопии.
В ней переменная временная задержка между интерферирующими
полями преобразовалась бы в соответствующее
пространственное распределение интенсивности,
регистрируемое не последовательно, как в обсуждаемом
аналоге, а одновременно. Такую регистрацию целесообразно
производить на ПЗС-матрицу, что удобно для ввода
в компьютер полученных экспериментальных данных
для последующей цифровой обработки.
Поиск
соответствующего прототипа естественно приводит
к голографии. Голографический вариант Фурье-спектроскопии
заключается в следующем
[4-5]. Две плоские
волны, образованные квазиточечным немонохроматическим
источником, направлялись на регистрирующую среду-фотопластинку
под углом 2θ. Зафиксированная на ней интерферограмма
(спектральная голограмма) представляла собою
сумму элементарных интерферограмм, образованными
отдельными спектральными линиями, содержащимися
в источнике. Нетрудно показать, что зарегистрированное
распределение интенсивности описывается косинусным
преобразованием Фурье от спектральной плотности
источника. При обратном преобразовании Фурье,
осуществляемом когерентной оптической системой,
на ее выходе возникает изображение точечных
источников, каждый из которых соответствует
отдельному спектральному компоненту, а распределение
их интенсивности – спектральной плотности анализируемого
источника. Однако быстрое изменение разности
оптических путей по голограмме автоматически
приводит к образованию высокочастотной пространственной
несущей. Она надежно разрешается голографическими
фотоэмульсиями, однако сопутствующий им фотопроцесс
существенно затрудняет автоматизацию и быстродействие
измерений. Именно поэтому цитированные работы
не получили широкого развития, хотя неявно содержащаяся
в них идея замены временного преобразования
Фурье на пространственное по-прежнему привлекательна
в связи с принципиальной возможностью устранения
отмеченных выше недостатков Фурье-спектроскопии.
Таким образом, разработка пространственного
аналога Фурье-спектроскопии сталкивается с неразрешимым
на первый взгляд противоречием между необходимостью
разрешения высокочастотной пространственной
модуляций на большой площади, что требует применения
фотоэмульсий и соответствующим им фотопроцесса.
Современная же элементная база - ПЗС-матрицы,
превосходящие высокоразрешающие фотоэмульсии
по чувствительности и удобные для непосредственного
ввода зарегистрированной информации в компьютер,
значительно уступает им по размерам и разрешающей
способности.
Значительный шаг в устранении
указанной трудности был сделан Дж. Харландером
с соавторами [6,7].
Они предложили способ преобразования высокочастотной
пространственной несущей в низкочастотную, в
результате которого для средней частоты исследуемого
спектра Vср получаемая пространственная частота
равна нулю и возрастает пропорционально разности
V-Vср. Таким образом, осуществляется «пространственное
гетеродинирование» несущей пространственной
частоты. Принципиальная оптическая схема соответствующего
спектрометра практически совпадает со схемой
хорошо известного спектрометра с интерференционной
селективной амплитудной модуляцией СИСАМом.
Его описание можно найти в любой достаточно
полной монографии по спектроскопии (см., например,
[1]). Отличие заключается в том, что в СИСАМе
запись необходимой информации осуществляется
точечным приемником последовательно во времени,
а в пространственном гетеродинном спектрометре
– сразу, единовременно, на ПЗС-матрицу. Следует
отметить, однако, что реализация описанного
метода затруднена. Действительно, регистрация
интерферирующих волновых полей квадратичным
детектором приводит, как обычно, к тому, что
при восстановлении спектра в плюс первом порядке
дифракции одновременно возникает сопряженный,
минус первый порядок. Нетрудно заметить, что
в данном случае они пространственно не разделены
и накладываются друг на друга. Для устранения
этого недостатка авторы
[10] предложили установить
дополнительный светофильтр, срезающий часть
спектра, а именно, с одной из сторон центральной
частоты Vср, что приводит к потери части информации,
если спектр не симметричен, да и изготовить
такой светофильтр с заданным резким краем проблематично.
В работе [8] пространственное гетеродинирование
осуществлялось с помощью диффузно рассеивающей
поверхности. Ее отражающие свойства позволили
получить изображение всей поверхности с изменяющейся
по ней разности оптических путей, но в то же
время обусловили появление спекл-шума, что ограничивает
область применения такого метода определением
длины когерентности.
В настоящей работе описывается
простая по сравнению с аналогами и малочувствительная
к вибрациям схема пространственного
 Фурье-спектрометра.
Преобразование высокочастотной пространственной
несущей в низкочастотную в ней осуществлялось
с помощью двойной голографической дифракционной
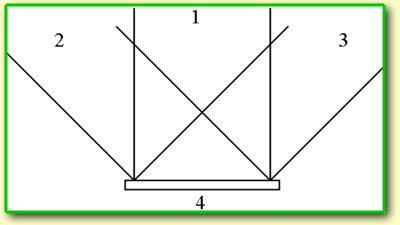
решетки, записанной по схеме (см. рис.).
Плоские волны 2 и 3 последовательно, двойной
экспозицией, с помощью опорной плоской волны
1 записывались на регистрирующую среду 4. Пучок
1 падал по нормали к поверхности голограммы,
углы падения пучков 2 и 3 составляли 45о.
Благодаря большой толщине фотоэмульсии, процесс
восстановления такой голограммы происходил за
счет дифракции Брэгга. В результате ее дифракционная
эффективность имела высокий уровень, а сопряженные
порядки дифракции практически отсутствовали.
Если направить на такую голограмму монохроматические
пучки 2 и 3, то восстановленные пучки совпадут
и будут распространяться по общему направлению.
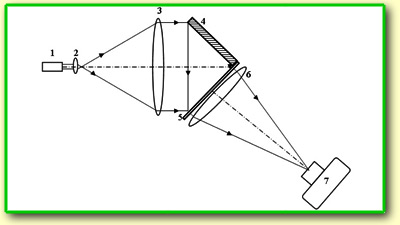
Оптическая схема пространственного Фурье-спектрометра
приведена на рисунке справа. Источником 1 исследуемого
излучения служил полупроводниковый лазер, мощностью
15 мВт со средней длиной волны 650 нм, работающий
в режиме нескольких аксиальных мод. Коллимированное
линзами 2,3 излучение направляли на двойную
дифракционную решетку 5 под углом 45о.
При этом половина коллимированного пучка попадала
на решетку после отражения от зеркала 4. Излучение,
дифрагированное на решетке, с помощью линзы
6 направляли во входной зрачок объектива цифрового
фотоаппарата 7. Фотоаппарат был сфокусирован
на поверхность голографического элемента 5 и
регистрировал картину интерференции двух пучков
на выходе дифракционной решетки. Разность хода
двух пучков близка к нулю в точке контакта решетки
с зеркалом 6 и линейно нарастала, если смещаться
вдоль решетки справа налево. С учетом высокой
пространственной когерентности лазерного излучения
можно полагать, что контраст интерференционной
картины, образованной пучками, отображал модуль
функции временной когерентности.
 Увеличенный
фрагмент зарегистрированной интерферограммы
показан на рисунке. Можно видеть, что контраст
(видность) интерференционных полос имеет периодический
характер, что указывает на наличие как минимум
двух достаточно выраженных максимумов в спектре
исследуемого излучения.
Для количественного
определения спектра излучения производили преобразование
Фурье от распределения интенсивности в исходной
интерферограмме. В принципе для этого достаточно
выполнить преобразования Фурье от распределения
интенсивности лишь по одной (в принципе, любой)
строке из отснятого кадра, поскольку интерференционные
полосы ориентированы перпендикулярно строкам
и на всех строках прорисовывают примерно одинаковое
распределение интенсивности. Однако с целью
усреднения шума выполняли двумерное преобразование
Фурье по всему кадру и лишь затем выбирали из
полученного двумерного массива одну строку,
содержащую информацию о спектре пространственных
частот исходной интерферограммы.
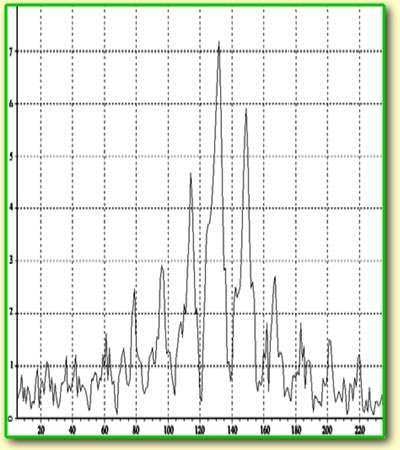 Полученный
график распределения спектра пространственных
частот (см. рис.) в определенном масштабе отображает
спектр исследуемого излучения.
Из графика
можно заключить, что спектр состоит из нескольких
равноотстоящих линий излучения. Исходя из геометрических
параметров схемы регистрации интерферограммы,
числа пикселей регистрирующей матрицы фотокамеры
и известной средней длины волны излучения (0,65
мкм) нетрудно подсчитать цену одного деления
на шкале длин волн (по горизонтали) графика.
Для условий проведенного опыта она составляет
1,02•10-10 м. Разница в длине волны
двух наиболее выраженных линий в спектре излучения,
как следует из графика (с учетом указанного
масштаба) составляет 17,34•10-10
м. Прямое измерение длины когерентности излучения
данного источника с помощью интерферометра Майкельсона
хорошо согласуется с этим результатом. В заключении
отметим, что, судя по литературным данным, включая
данную работу, в настоящее время в рамках Фурье-спектроскопии
развивается новое перспективное направление
– пространственная Фурье-спектроскопия, более
предпочтительное по сравнению со своим временным
аналогом для исследования быстропротекающих
процессов.
Литература.
1. Светосильные спектральные приборы/под
ред.К.И. Тарасова. М.:Наука,1988 г.,263 с.
2. Р. Дж. Белл. Введение в Фурье-спектроскопию.
М.: Мир, 1975, 380 с.
3. Крылов А.С., Втюрин
А.Н., Герасимов Ю.В. Обработка данных инфрокрасной
Фурье-спектроскопии. Методич. пособие. Препринт
№832 Ф. Красноярск, Институт физики СО РАН,
2005, 48 с.
4. Дж. Строук. Введение в когерентную
оптику и голографию – М.: Мир, 1967, 347 с.
5. Оптическая голография/под ред. Г. Колфилда.-
М.: Мир, 1982, т.2, с. 647-655.
6. Harlander
J.M, Roester F.L., Cardon J.G., at all Appl.
Opt., 2002, 41, №7, p. 1343-1352.
7. Engelert
C.K., Harlander J.M, Cardon J.G. Roeseler F.L.,
Appl Opt., 2004, v.43, №36, p. 6680-6687.
8. Власов Н.Г., Крицкий А.В. IX Научн. конф.
МГТУ «Станкин», 2006,, с. 263-264.
|
